Georgy Ball, Vladislav Medintsev

Modern methods of formalized descriptions in human sciences can be grouped according to their development strategies.

The first strategy: on the basis of laws described in "humanitarian" language, to choose appropriate mathematical models (Mesarovic, 1978; Lefebvre, 1991).

The second strategy: on the basis of particular types of mathematical models used in physics, biology and other natural sciences, to seek the possibility of applying such models in human sciences (Ryzhov, 2010; Petrenko, Suprun, 2014).

The third strategy: on the basis of the most general mathematical models, to seek possibility of their use in human sciences. This strategy seems to have not yet become widespread.

We use a third strategy. In our set-theoretic method of process description (S-method) the most general mathematical apparatus (set theory) is applied to the most general humanitarian concept of "culture", and components (modi) of culture are represented as algebraic structures.

In developing the S-method we aim, among other things, to the accessibility of the method for its use by experts in various human sciences. The most complete description of the method has been published in the book

A method of set-theoretic description of processes and its applications in psychology (2016, in Russian)

Linked publications

The method of set-theoretic description of processes: applying in the intellect study (2017).

Essentials in S-method for process description (2017).

Main in S-method

We proceed from the fundamental set theory statements, in particular from the concept of structure. To determine the structure (S), a relationship among elements is defined:

S = <M; R₁, R₂, R₃, … >,                (1)

where

M – basic set, M = {a, b, c… };

R₁, R₂, R₃ ... – relations among elements.

General description of structures in set theory (1) we specify to describe the algebraic structures, using set-theoretic representation of mapping

The mapping, in general, is the following record:

Function : Prototype → Image

where the symbol ":" ties functional (Function) and matter (Prototype, Image) components of mapping.

For example, a mathematical function y = x² as a form of mapping is following:

Squaring a number : Set of numbers 1 → Set of numbers 2.

Non-mathematical transformation can also be described as mapping, for example:

Sociological science : Social practice → Scientific knowledge about social practices

Or

Science methodology : The phenomena of being → Scientific knowledge

The components of mapping – Function, Prototype, Image – are presented as modi, interpreted as structured sets of elements. These elements can also be considered as modi below in the hierarchy.

A process is a change, it takes place in time. So, we assume that Prototype precedes Image.

Mathematical space of mappings covers all theoretically possible mappings, which involve modi considered by the researcher.

We use an algebraic record of math. spaces of mappings. For example, the record of math. space for the two modi A and B is the following:

{А; B} : {А; B} → {А1; B1}                   (2)

The elements of the set {A, B} are also regarded as sets.

We consider the math. space of mappings as a structure in which:

1. Modi (sets) A and B in (2) are the main elements of the set structures as well as relationships defined on this set.

2. Prototype and Function are identical, as defined in the same time moment. Modus Function or some of its constituents is considered as an expression of the relationship between the components of this structure.

3. Images, in general, are different from the Prototypes, that is reflected by index numbers (A1, B1).

Equation (2) is a record of a complex mapping with A and B modi. It is also a generalized record of eight simple following mappings:

A complex mapping can be represented as a three-dimensional matrix (table), which is a graphic representation (Fig. 1) of math. space (2).

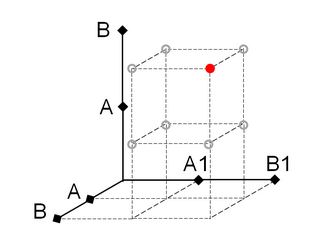
Fig. 1

This math. space of mappings contains 8 points, red highlighted point corresponds to following mapping

B : B → B1

To illustrate the application of 2-modi mapping in psychological studies, we denote modus of psychic representations as Psy (psychic modus or component), modus of non-psychic phenomena as Ph (phenomenal modus).

Then, as in (2), the record of math. space with Psy and Ph modi will be the following:

{Psy; Ph } : {Psy; Ph} → {Psy1; Ph1}                   (3)

This math. space contains 2³ = 8 points, each of which defines one of the following simple mappings.

We give some examples of processes described by these mappings.

Psy : Psy → Ph1 – processes of motivational, volitional, emotional regulation of any kind of practice; the implementation of them in person's value orientations and beliefs.

Psy : Ph → Ph1 – processes of production and research activities, as well as arts.

Mathematical space of mappings may be further considered, in particular, as a theoretical model of the investigated phenomena.

In a specific study it is necessary to determine the most efficient set of modi – the components of processes focused by researchers.

Mathematical space of mappings which contains more than two modi can be obtained in a way of detailing 2-modi math. space or in the very beginning of the study. The more modi are selected, the more points are in the space of mappings, the more detailed description of the scientific phenomena becomes, but the greater is the amount of data to be analyzed.