Исходим из основных положений теории множеств, в частности понятия структура. Чтобы определить структуру (S), задают отношения, в которых находятся её элементы.

S = <M; R₁, R₂, R₃, … >,                (1)

где

M – основное множество M={a, b, c…};

R₁, R₂, R₃, … – заданные на этом множестве отношения.

Общую запись структур в теории множеств (1) конкретизируем  для описания алгебраических структур, используя теоретико-множественное понятие отображение.

Отображение, в общем, является записью следующего отношения трёх компонентов

Функции : Прообразы → Образы,

 где символ «:» связывает функциональные (Функция) и предметные (Прообраз, Образ) компоненты отображения.

Например, запись математической функции y = x² в форме отображения множеств будет такой:

Возведение числа в квадрат : Множество чисел 1 → Множество чисел 2.

Как отображения можно записать нематематические преобразования, например:

Социологическая наука : Общественные практики → Научные знания об общественных практиках

Методология науки : Феномены бытия → Научные знания

Компонентами отображения – функция, прообраз, образ – представлены модусы, трактуемые как структурированные множества элементов. Эти элементы могут быть также рассмотрены как модусы, находящиеся ниже в иерархии.

Поскольку процесс – это изменение, и происходит оно во времени, то, используя отображение для описания процесса, мы подразумеваем, что прообраз предшествует образу.

Математическое пространство отображений охватывает все теоретически возможные отображения, в которых участвуют рассматриваемые исследователем модусы.

Будем использовать алгебраические записи математических пространств отображений. Например, запись пространства для двух модусов А и Б будет такой:

{А; Б} : {А; Б} → {А1; Б1}                   (2)

В этой записи, как принято в теории множеств, в фигурные скобки заключены элементы множеств. Элементы множества {А; Б} также рассматриваем как множества.

Далее рассматриваем математическое пространство отображений как структуру, в которой:

1. Модусы (множества) А и Б  в (2)  могут быть элементами основного множества структуры и отношениями, заданными на этом множестве.

2. Множества модусов-прообразов и модусов-функций тождественны, так как определены на один и тот же (начальный) момент этапа. Модусы-функции или некоторые их компоненты рассматриваем как выражение отношений между компонентами этого пространства.

3. Множества-образы, в общем случае, отличны от множеств-прообразов, что отражено цифровыми индексами (А1; Б1).

Формула (2) является записью сложного отображения модусов А и Б. Она является также обобщённой записью восьми простых отображений, которые также можно представить алгебраическими записями..

Отображения можно представить в виде трёхмерной матрицы (таблицы). На Рис. 1. показано такое (графическое) представление математического пространства отображений формата {А; Б}.

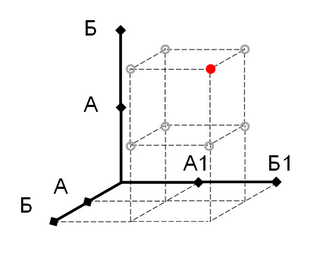
Рис. 1

Это математическое пространство отображений образуют 8 точек – красным цветом выделена точка, соответствующая отображению

Б : Б → Б1

Проиллюстрируем использование двухмодусного пространства отображений на психологическом материале.

– модусы, представленные в психике, обозначим символом Пси (психический модус или компонент);

– модусы, описывающие непсихические феномены обозначим Ф (феноменальный модус).

Тогда, подобно (2), обобщённой записью математического пространства с модусами Пси и Ф будет следующая

{Пси; Ф} : {Пси; Ф} → {Пси1; Ф1}                   (3)

Описываемое пространство содержит 2³=8 точек, каждая из которых определяет одно из следующих простых отображений.

Приведём примеры процессов, описываемых этими отображениями.

Пси : Пси → Ф1 – процессы мотивационной, волевой, эмоциональной регуляции любого вида практической деятельности, осуществление в ней ценностных ориентаций и верований.

Пси : Ф → Ф1– процессы производственной и научной деятельности, а также художественного творчества.

Математическое пространство отображений может быть далее рассмотрено, в частности, как теоретическая модель исследуемых явлений, в том числе в психологии.

В конкретном исследовании необходимо определиться с наиболее рациональным выделением модусов – компонентов интересующих исследователя процессов.

Математические пространства отображений, содержащие более двух модусов, могут быть получены детализацией модусов двухмодусного пространства или определены уже в начале исследования. Чем больше модусов выделено, тем больше точек в пространстве отображений, тем более детальным становится описания научных феноменов. Но и тем больший объём данных необходимо анализировать.